-
[轉貼]球面天文學
Posted by yfsum on 3 1 月, 2006 在 7:56 上午http://home.kimo.com.tw/shpao5824/sph_astro.htm
球面天文學
天文學是一門很古老的科學。由於天象的複雜程度遠遠超過肉眼觀測所能理解,因此對於天文穿鑿附會的歷史證據比比皆是。儘管今天以邁入二十一世紀,天文在許多地區仍然具有神秘的色彩。
目前天文學發展比較好的國家,大部分都是從事航太科技發展的國家。由於天文物裡的範疇太大,不太適合以網頁的形式呈現。因此我們主要的目的是以球面天文學為主要的訴求。球面天文學主要是以時間、座標系統與軌道動力學結合的學門。有了這項技術後,可以應用在天文望遠鏡的精密定位與星體自動導入、同步追蹤。複雜一點的應用可用於航海導航與極精密的指向定位,目前這些技術大都用於人造衛星導航、彈道導引與其他國防用途。至於軌道動力學則用於分析設計人造衛星運行軌道或彈道飛彈的落點分析。
球面天文學的發展很早。它的基本工具是三角幾何學與向量的運用。雖然這些數學工具十分簡單,但是要正確地認知並使用並不是那麼容易。目前在國內鮮少有相關的資訊來介紹這個實用的科學,因此我把在台北市立天文館工作四年的部分成果與參考資料和大家分享,希望對於有興趣的人能有幫助。
假設讀者已有基本的向量分析、球面三角學、天體的座標概念與電腦程式的編寫的能力。此外為了盡量避免較為冗長的數學方程式,完全透過實際的範例來說明重要的公式運用。由於不希望它是一本教科書,而是實用的參考手冊。網頁裡的許多數學式子與範例都由我先做過一次,然後再整理後放在網頁裡,錯誤之處在所難免,若遇到不符合的地方請麻煩告之。
目前我把球面天文學分成幾個常用的部分,希望能更為簡單明瞭。由於內容基於使用的便利性,所以計算獲得的精密度有所保留。 儘管如此, 對於一般的天文觀測而言,這些計算的精度使用起來已綽綽有餘。這裡提供的方法都是最重要且實用的部分,若是希望能提高計算的精度,則必須投入一些精力來研究多體運動與攝動理論。若是這些複雜的篇幅整理好,往後會陸續地加入。
1154248456 replied 14 年, 5 月 前 6 Members · 16 Replies -
16 Replies
-
http://home.kimo.com.tw/shpao5824/unit.htm
球面天文計算常用單位
時間與角度的換算 24h = 360°
1h = 60m = 3600s
1° = 60′ = 3600”
勁度與角度的換算 π=3.1415926 rad =180°
範例
某星體的赤道座標 (13h25m16s , 15° 6′ 36” )
13h25m16s=13.4211111h = 201.3166667°
15° 6′ 36”=15.11°
台北的地理座標 (E121° 31′ 48” ,N25° 4′ )
E121° 31′ 48” = 121.53° = 8.102h = 8h6m7.2s
由此可看出台灣的時差是 8小時,位於中原標準時區。
[ 本帖最後由 yfsum 於 2006-1-3 04:04 PM 編輯 ]
-
http://home.kimo.com.tw/shpao5824/time.htm
時間
(1) 年與日的定義
太陽年
365.24219太陽日,又稱回歸年。太陽由春分到下次春分的時刻。通常作為曆法的依據。
恆星年
365.256363太陽日。太陽實際在空間中公轉一週的時間。
近點年
365.259636太陽日。太陽由近日點到下次通過近日點的時間,是軌道計算所需求的時間單位。
恆星日
某個恆星(無自行運動)連續兩次過中天的時間間隔,稱為一個恆星日。一個恆星日約為23小時 56 分 4 秒。若是透過望遠鏡的赤道儀同步追蹤來拍攝恆星的話,追蹤馬達必須以23小時 56 分 4 秒旋轉360度的速度來追蹤,因此我們稱此為恆星時追蹤模式。
儒略日 ( Julian Day 或簡稱 JD )
儒略日的起算點4713BC GMT(UT)12h0m0s。每過一個太陽日,則累加上一日。因此 1900年一月一日世界時0時,訂為儒略日第2415020。或記為 JD1900.0=2415020日。同理JD2000.0=241545日。有時候我們會使用儒略世紀(Julian Century),就是將儒略日除以36525。
[ 本帖最後由 yfsum 於 2006-1-3 04:04 PM 編輯 ]
-
JD=年份+月份+日+( 時間 – 時差 )/24-1.5+241545
儒略世紀=( JD- JD1900.0 )/ 36525 就是指距離1900年一月一日世界時0時的儒略世紀
範例
2001年6月12日17:19
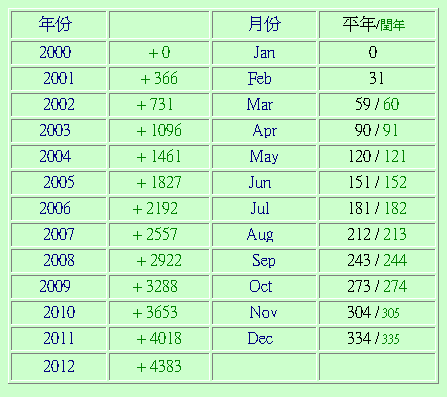
查儒略日表 2001年份=366 6月份=151 日=12 時間=17.32h 台灣時差=8h
JD=366+151+12+(17.32 – 8)/24 –1.5+241545=242072.388
太陽日
太陽連續兩次過中天的時間間隔,稱為一個太陽日。由於地球繞日運動不均勻的速度,因此我們都使用平均太陽日來替代真實的太陽日。平均太陽時就是手錶時間,一個平均太陽日等於24小時,等於1440分,也等於86400秒。
(2) 時間計算
(a) UT (Universal Time) 格林威治標準時或世界時
LT ( Local Time) 地方時
不管 UT 或是 LT 均以平均太陽時制訂。
LT=UT+時差
(b) GMST(Greenwich Mean Sidereal Time)格林威治平均恆星時
LMST(Local Mean Sidereal Time) 地方平均恆星時,或說為「過當地中天子午圈的赤經值」
由於地球繞日公轉的角度每日不同以及歲差與章動的影響,因此實際的恆星時不容易計算,所以我們可以用平均恆星時來替代。對於精度要求不高的觀測,平均恆星時會方便許多。 在格林威治 0h0m0s 的時候,平均恆星時的計算如下:
GMST=6h41m50.4841s+ 8640184.81266×( JD-JD2000.0 )/36525.24 s
若觀測者在不同位置、不同時間,地方平均恆星時的轉換如下:
LMST=GMST+ λ +( LT – 時差 )×1.002738
λ 為地理經度,以台北為例 ( 東經121°31’4” ) = 8h6m4.3s 時差=8h
1.002738是把太陽時轉成恆星時的轉換常數。
(c) RST(Real Sun time)真太陽時
MST(Mean Sun time)平均太陽時
RST是根據真太陽,在天空的位置定時間,以太陽過中天子午線為12h, 由於軌道面的傾斜(23°44)與公轉不均造每日的間隔不同。因此使用起來十分不方便。
MST為鐘錶用時間,以理想的太陽( 以半徑1AU,等速度沿赤道圓等速運動繞行地球 )過中天來定義MST的12h。
真太陽時的計算頗為複雜,不過它卻是天文計算裡非常重要的資料。真太陽日正午十二時,太陽一定過中天,而平均太陽時則否。真太陽時與平均太陽時會有略微的差異,這個差異我們訂為均時差。
E =RST-MST 稱為均時差,每年略有不同,JD2000年的均時差如下(使用儒略日表):
L=279.729+0.985647?[月份+日+( 地方時間-時差)/24]
E = -107.5sinL+596.1sin2L+4.4sin3L-12.7sin4L-428.5cosL-2.1cos2L+19.3cos3L
由於地理位置的關係,若是地理經度並不位於標準的時差經度,必須考慮地理位置的修正值才能換算MST與RST。
MST=RST+(λ- 時差)+E
(d) GAST(Greenwich Apparent Sidereal Time)格林威治恆星時
LAST(Local Apparent Sidereal Time)地方恆星時
與 GMST 類似,但處理起來較為繁瑣( 需校正歲差、公轉速率與章動 ),GST必須以程式精密計算。
ET( Ephemeris Time ) 力學時
我們所使用的太陽時間,如UT,都是與地球自轉相關。很可惜的是,地球自轉的速率並不如預 期的規則。因此當地球運轉的誤差接近一秒時,為了生活與作息之用,我們採取閏秒的作法使時間與太陽的位置相配合。但是這樣一來卻造成了UT(或手錶時間)的不規律性。目前大部分的天體計算都採用 ET 來替代 UT 。
UT=ET-△T
若是年代很久遠(數個世紀之隔)
△T=0.41+ 1.2053T + 0.4992T2 T( 儒略世紀 ) =( JD- JD1900.0 )/ 36525
若是年代不遠(1900~ 2000),目前尚無理論推算,因此必須藉由實際觀測來修正。修正值如下:
年份 ΔT (分鐘)
1903 0.0
1912 0.2
1927 0.4
1940 0.4
1950 0.5
1965 0.6
1977 0.8
1987 1.0至於1997年則為 63秒,2001年為65秒。往後仍未知??
-
http://home.kimo.com.tw/shpao5824/coordinate.htm
座標系統
地理座標
(γ,ψ)以地球的地理經度與緯度定義的座標系,座標零點在格林威治。
黃道座標
(λ,β)以地球繞行太陽的平均公轉平面為基準面,零點採用春分點。
赤道座標
(α,δ)以地球的平均赤道面延伸為基本面,座標零點為春分點。
地平座標系
(A,h)以觀測者的方位與仰角定義的座標系,座標零點為北方。
黃道與赤道座標系統的互換
黃赤道交角 I=23°26’21.448″
赤道座標轉成黃道座標:
sinλ= sinαcosI+tanδsinI
cosλ= cosα
sinβ= sinδcosI–cosδsinαsinI
黃道座標轉成赤道座標:
sinα= sinλcosI–tanβsinI
cosα= cosλ
sinδ= sinβcosI+cosβsinλsinI
地平座標系統與赤道座標系統的互換
赤道座標轉成地平座標座標:
t = LMST – α
sinh = sinψ sinδ+ cosψ cosδ cost
cosh sinA= – cosδ sint
cosh cosA= cosψ sinδ-sinψ cosδ cost
地平座標轉成赤道座標:
sinδ = sinψ sinh – cosψ cosh cosA
cosδ sint = –cosh sinA
cosδ cost = –sinh cosψ– cosh sinψ cosA
α = LMST – t
範例
座標系統的變換最複雜的就是地平座標系,若是能夠瞭解地平座標與赤道座標之間的轉換,其它的部分相對而言就非常簡易了。因此我們以赤道座標轉成地平座標為例。
觀測時間:2001年12月10日 22:00
觀測位置:台北( E121.5° , N25°)
觀測天體:天狼星(赤經 6h45m8.9s,赤緯 -16°42’58”)
參考『球面天文學區』的 單位 與 時間 專文,2001年12月10日 22:00 的儒略日計算如下:
2001年12月10日22:00
查儒略日表 2001年份=366 12月份=334 日=10 時間=22h 台灣時差=8h
JD=366+334+10+(22 – 8)/24 –1.5+241545=242254.08333
格林威治恆星時與地方恆星時計算如下:
在格林威治 0h0m0s 的時候,平均恆星時的計算如下:
GMST=6h41m50.4841s+ 8640184.81266×( JD-241545.0 )/36525.24 s
若觀測者在不同位置、不同時間,地方平均恆星時的轉換如下:
LMST=GMST+ γ +( 觀測時間- 時差 )×1.002738
γ為地理經度,以台北為例 ( 東經121.5°) = 8h6m 時差=8h
GMST= 5.2924 h = 79.3859°
LMST= 3.4307 h = 51.4609°
座標變換公式
赤道座標轉成地平座標座標:
α=6h45m8.9s=101.287° δ= -16°42’58” =-16.716° ψ=25°
t = LMST – α
sinh = sinψ sinδ+ cosψ cosδ cost
cosh sinA= – cosδ sint
cosh cosA= cosψ sinδ-sinψ cosδ cost
t= 310.201°
sinh=0.438 h=26°
sinA=-0.81372
cosA=0.5813
經過象現判斷 A=125.5°(由北方順時針起算。北方0°,東方90°,依此類推 )。
所以天狼星在2001年12月10日22:00,由台北觀測時,它位於北偏東125.5°,仰角26°
備註:
因為計算之中使用平均恆星時,同時使用天狼星的JD2000.0的分點座標,因此結果會與實際位置有點偏差。
經過以上真實恆星時,與瞬時分點座標轉換的修正:
可以得知更為精密的資料為 A=124.5° , h=27.06° ,經大氣折射修正後 h=27.1°
-
http://home.kimo.com.tw/shpao5824/pre_nut.htm
章動與進動
進動(Precession)
由於地球的外型成微扁又上下凹陷的「梨」形。因此當受到太陽傾斜23.5度的引力時,會產生不對稱的引力,這個引力對於地球的運動造成擾動的力矩。我們知道有轉動體受到外加的力矩後,會產生角動量變化。這個現象我們稱為進動。地球的進動速率不會太快,它的運動週期約25600年。換句話說,我們制訂的黃道與赤道交角稱為春分點,這也是赤道座標系統與黃道座標系統的參考點。由於春分點受到進動的影響,會沿著赤道面滑動,其週期為25600年。因為參考點的移動,致使我們定義天體的座標位置變的不可靠。目前的作法就是採用固定的分點來製作星圖,例如1950年或是2000分點的星圖。如果使用者要運用星圖時,必須自行轉換至瞬時分點的座標系統,以獲得合理的觀測理論值。分點修正的技巧只牽涉到簡單的矩陣運算,因為它不過是一個座標旋轉的問題而已。詳細的作法可以參考「天體動力學概說」裡頭「天文計算概論」的網頁。
章動(Nutation)
相較於進動的問題,章動顯的較為細小。章動發生於無外加力矩的時候(Torque Free),但是旋轉體仍然可以像進動一般地自由旋轉。不過這個旋轉方式與進動差異很多,因為每個軸向的角動量雖然不守恆,但是三軸的總角動量是守恆的。所以三軸的角動量分配與轉動體的三軸轉動慣量息息相關。一般我們所使用的天球座標,如黃道面與赤道面的定義都不考慮章動的影響,所以嚴格來講,它們應該稱為「平均黃道面」與「平均赤道面」。經過章動修正後,才能算是正確的座標平面,也才合乎瞬時座標的定義。
當一個星體經過進動與其自行運動(Proper motion)修正後的赤道座標值(α,δ),我們可根據以下的方法來進行章動的修正。
時間
T=(JD-2415020)/ 36525
太陽的平均經度
L=279.6967+36000.7689T+0.000303 T2
月球的平均經度
l=270.4342+481267.8831 T-0.001133 T2
太陽的平均近日點離角
M=358.4758+35999.0498 T-0.00015 T2
月球的平均近日點離角
m=296.1046+477198.8491 T+0.009192 T2
月球的升交點經度
Ω=259.1833-1934.142 T+0.002078 T2Δψ=-(17.2327+0.01737 T) sin(Ω)-(1.2729+0.00013 T) sin(2L)+0.2088 sin(2Ω)
-0.2037 sin(2l)+(0.1261-0.00031 T) sin(M)+0.0675 sin(m)-(0.0497-0.00012 T) sin(2L+M)
-0.0342 sin(2l-Ω)-0.0261sin(2l+m)+0.0214 sin(2L-M)-0.0149 sin(2L-2l+m)
+0.0124 sin(2L-Ω)+0.0114sin(2l-m)Δε=(9.21+0.00091 T) cos(Ω)+(0.5522-0.00029 T) cos(2L)-0.0904 cos(2Ω)
+0.0884 cos(2l)+0.0216 cos(2L+M)+0.0183 cos(2l-Ω)
+0.0113 cos(2l+m)-0.0093 cos(2L-M)-0.0066 cos(2L--Ω)黃赤道面交角 ε=23.452294-0.0130125 T-0.00000164 T2+0.000000503 T3
赤經與赤緯的修正量
Δα=[cos(ε)+sin(ε) sin(α) tan(δ)] Δψ-cos(α) tan(δ) Δε (arcsec)
Δδ=sin(ε) cos(α) Δψ+sin(α) Δε (arcsec)範例
2000年9月1日 10:30 經過歲差與自行運動修正過後的星體座標(2h42m44.8s,49° 8’24.4”),轉成瞬時座標?
時間
JD=2451788.60490741T=1.00666953887502
太陽的平均經度
L=36520.5744347645
月球的平均經度
l=484748.151007472
太陽的平均近日點離角
M=36597.6225100975
月球的平均近日點離角
m=480677.65929021
月球的升交點經度
Ω=-1687.85642944778Δψ=-15.3991
Δε=-2.91086
黃赤道面交角 ε=23.439194
赤經與赤緯的修正量 Δα=-16.193 arcsec=-1.08 s
Δδ=-6.542 arcsec星體座標經章動修正後的的赤經與赤緯(2h42m43.72s,49° 8’17.858”)
-
http://home.kimo.com.tw/shpao5824/sun.htm
太陽位置計算
計算太陽的位置可以推估日出沒時間,節氣等相關資料。精密的太陽位置計算必須修正許多行星引起的擾動,由於計算十分冗長,所以在此只提供最基本的計算方法。對於一般觀測而言,此計算已能足夠的精密度。但若是涉及曆法與座標系統的校正,則需進一步引入攝動的修正項。
計算時間
時間 JD1= JD-JD2000.0
距離2000年的儒略世紀 T=(JD-JD2000)/ 36525
軌道資料
軌道週期 P=1.00004回歸年
距離春分點平均離角 ε=280.466457+0.985647358 JD1+0.000304 T2
近地點離角 ω=282.937348+0.00004707624 JD1+0.0004569 T2
軌道偏心率 E=0.01670862-0.00004204 T
軌道半徑 A=1.00001161 AU
計算結果
近日點平均離角 M=ε-ω
利用級數展開的克卜勒方程式(Kepler’s Equation)求得真實的近日點離角
ν=M+360 E sin(M)/π+900 E2 sin(2M)/4π-180E3sin(M)/ 4π
太陽的黃道經度 λ=ν+ω
因為太陽在黃道面上運動,所以太陽的黃道緯度 β=0
若需要太陽的赤道經度與緯度,可參考座標系統的變換部分。將黃道座標轉成赤道座標。或者更進一步轉成地平方為角。
範例
2000年9月1日 AM10:30 太陽的黃道經緯度 、赤道經緯度 與地平方為角
計算儒略日得到 JD=2451788.6049
JD1=243.6049
儒略世紀 T=0.00667
軌道資料
ε=520.492123°
ω=282.948812°
E=0.01671
計算結果
M=237.543311°
λ=158.895° β=0°
經過黃道座標與赤道座標系統轉換後
α=10h42m
δ=8°14′
經過地平座標轉換後
A=99°
h=37°
若是經過其他行星的攝動修正項和章動修正後的黃道座標與赤道座標值
λ=158.9639°
α=10h42m15s
δ=8°12’31”
-
行星位置計算
以下所列的計算公式基於視覺的清晰,因此沒有深入說明。若需要瞭解進一步的使用請參考最後的範例。這裡的計算方法並沒有考慮到攝動的修正,因此木星以外的位置計算誤差會越來越大。目前筆者已經完成部分天體計算的程式,位置計算的精密度大概在10個秒角以下。有需要的話,可以免費來 e-mail 索取。
軌道六元素
升交點引數(Ω)
軌道傾角(i)
近日點引數(ω)
軌道半長軸(a)
軌道偏心率(e)
時間(t)
星體軌道資料 查JD2000行星軌道元素表(本頁最下方)
ε=A1+A2?MJD+A3?T2
ω=B1+B2?T+B3?T2
e =C1+C2?T+C3?T2
i =D1+D2?T+D3?T2
Ω=E1+E2?T+E3?T2
a =F1+F2?T+F3?T2
Tp =G1+G2?T+G3?T2
地球的軌道資料
Te = 1.00004
εe = 100.466457+0.985647?MJD+0.0003032?T2
ωe = 102.937348+0.00004707624?MJD+0.0004569?T2
E = 0.01670863 -0.000042037?T
A=1.0

步驟三
sinΨ= sin( l -Ω)?cos( i )
cosΨ=cos( l -Ω)
經過反三角轉換可以得到 Ψ
步驟四
σ= sin-1[sin( l -Ω)?sin(i)]
S = r?cosσ
N=Ψ+Ω
步驟五

為了方便說明以上公式的使用,以一個範例來對照,並探討公式裡參數的意義。
範例
2001年6月12日17:19 觀測木星 觀測位置(台北) = (121.5°, 25°)
步驟一 查儒略日表 2001年份=366 6月份=151 日=12 時間=17.32h 台灣時差=8h
儒略日 JD=366+151+12+(17.32 – 8)/24 –1.5 +241545 = 242072.889
儒略世紀 T=0.014445
世界時 0h 格林威治平均恆星時 GMST=17.386h=260.787°
地方平均恆星時 LMST=10.848h=162.719°
步驟二 查木星軌道元素表 A~G的係數
行星平均春分點離角 ε=78.235°
近日點引數 ω=14.355°
軌道偏心率 e=0.0485
軌道傾角 i=1.3°
升交點引數 Ω=100.48°
軌道半徑 a=5.203
地球平均春分點離角 εe=620.779°
地球近日點引數 ωe=102.9622°
地球軌道偏心率 E=0.01671
步驟三
行星平均近日點離角 m=63.88°
行星軌道面經度 l=83.3565°
行星近日點離角 ν=69.002°
行星與太陽的距離 r=5.102
地球平均近日點離角 M=157.817°
地球軌道面經度 L=261.488°
地球近日點離角 νe=158.5255°
地球與太陽距離 R=1.0155
步驟四
sinΨ=-0.2943
cosΨ=0.9557 Ψ=342.8815°
σ=-0.006696°
S=5.1016
N=83.361°
木星為外行星 黃道經度 λ=83.0498° 黃道緯度 β=-0.32°
步驟五
將(λ,β)轉成(α,δ)
sinδ=0.39 赤道緯度 δ=22.94° =22°56’24”
sinα=0.913
cosα=0.0123 判斷象限後得到赤道經度 α=82.45° =5h29m48s
步驟六
地方時角 t=LMST-α=80.269°
sinh=0.0079 地平仰角 h=17.83°
sinA= -0.9
cosA= -0.43 地平方位角 A=287.55°
因此,我們可以在北偏東65度,仰角0.4度看到木星。
說明:若是經過多項的攝動計算後,行星的位置會更精確,它的赤道座標位置:
α=5h 29m54s
δ=22°57′ 21”
JD2000行星軌道元素
行星位置計算以下所列的計算公式基於視覺的清晰,因此沒有深入說明。若需要瞭解進一步的使用請參考最後的範例。這裡的計算方法並沒有考慮到攝動的修正,因此木星以外的位置計算誤差會越來越大。目前筆者已經完成部分天體計算的程式,位置計算的精密度大概在10個秒角以下。有需要的話,可以免費來 e-mail 索取。
軌道六元素
升交點引數(Ω)
軌道傾角(i)
近日點引數(ω)
軌道半長軸(a)
軌道偏心率(e)
時間(t)
星體軌道資料 查JD2000行星軌道元素表(本頁最下方)
ε=A1+A2?MJD+A3?T2
ω=B1+B2?T+B3?T2
e =C1+C2?T+C3?T2
i =D1+D2?T+D3?T2
Ω=E1+E2?T+E3?T2
a =F1+F2?T+F3?T2
Tp =G1+G2?T+G3?T2
地球的軌道資料
Te = 1.00004
εe = 100.466457+0.985647?MJD+0.0003032?T2
ωe = 102.937348+0.00004707624?MJD+0.0004569?T2
E = 0.01670863 -0.000042037?T
A=1.0

步驟三
sinΨ= sin( l -Ω)?cos( i )
cosΨ=cos( l -Ω)
經過反三角轉換可以得到 Ψ
步驟四
σ= sin-1[sin( l -Ω)?sin(i)]
S = r?cosσ
N=Ψ+Ω
步驟五

為了方便說明以上公式的使用,以一個範例來對照,並探討公式裡參數的意義。
範例
2001年6月12日17:19 觀測木星 觀測位置(台北) = (121.5°, 25°)
步驟一 查儒略日表 2001年份=366 6月份=151 日=12 時間=17.32h 台灣時差=8h
儒略日 JD=366+151+12+(17.32 – 8)/24 –1.5 +241545 = 242072.889
儒略世紀 T=0.014445
世界時 0h 格林威治平均恆星時 GMST=17.386h=260.787°
地方平均恆星時 LMST=10.848h=162.719°
步驟二 查木星軌道元素表 A~G的係數
行星平均春分點離角 ε=78.235°
近日點引數 ω=14.355°
軌道偏心率 e=0.0485
軌道傾角 i=1.3°
升交點引數 Ω=100.48°
軌道半徑 a=5.203
地球平均春分點離角 εe=620.779°
地球近日點引數 ωe=102.9622°
地球軌道偏心率 E=0.01671
步驟三
行星平均近日點離角 m=63.88°
行星軌道面經度 l=83.3565°
行星近日點離角 ν=69.002°
行星與太陽的距離 r=5.102
地球平均近日點離角 M=157.817°
地球軌道面經度 L=261.488°
地球近日點離角 νe=158.5255°
地球與太陽距離 R=1.0155
步驟四
sinΨ=-0.2943
cosΨ=0.9557 Ψ=342.8815°
σ=-0.006696°
S=5.1016
N=83.361°
木星為外行星 黃道經度 λ=83.0498° 黃道緯度 β=-0.32°
步驟五
將(λ,β)轉成(α,δ)
sinδ=0.39 赤道緯度 δ=22.94° =22°56’24”
sinα=0.913
cosα=0.0123 判斷象限後得到赤道經度 α=82.45° =5h29m48s
步驟六
地方時角 t=LMST-α=80.269°
sinh=0.0079 地平仰角 h=17.83°
sinA= -0.9
cosA= -0.43 地平方位角 A=287.55°
因此,我們可以在北偏東65度,仰角0.4度看到木星。
說明:若是經過多項的攝動計算後,行星的位置會更精確,它的赤道座標位置:
α=5h 29m54s
δ=22°57′ 21”
JD2000行星軌道元素
[ 本帖最後由 yfsum 於 2006-1-3 04:29 PM 編輯 ]
-
http://home.kimo.com.tw/shpao5824/moon.htm
月球位置計算
月球的位置計算是所有天體計算裡比較複雜的部分。往往為了提高一點計算的精確度,必須使用數百個擾動修正項,目前這些修正項在許多專業的天文書籍裡都找得到。由於月球每天在天空移動的數度很快,因此計算時間的正確性要求的比較多。之前計算太陽與行星時,都採用地方平均太陽時,但是計算月球位置必須採用力學時來減低誤差。這裡提供的方法,月球位置的誤差約小於1/15度。雖然在許多觀測上,這個精密度可能稍嫌不足,但是卻能夠簡單地推算月球的位置也算是實用的方法。
雖然月球繞行地球公轉,但是嚴格說起來,月球應該看成繞太陽運行。由於受到地球的擾動,所以月球以蛇行的方式環繞太陽。月球的軌道面會產生很大的位移,這也是他與其他行星最大的不同點。因為迅速移動的軌道面,造成實際計算非常不易。大致來說,月球相對於黃道面的軌道進動週期為18.6年(如同地球的歲差,我們又稱為升交點進動)。月球的近日點也會週期性的運動,主要的項次約為8.85年。另外月球繞地運行的軌道半徑每年約增加數公分之多。
計算時間
時間 JD1= JD-JD2000.0
說明:這裡的JD是使用力學時(ET)來計算,相關的資料請參考「時間」的網頁。
距離2000年的儒略世紀 T=(JD-JD2000)/ 36525
太陽的軌道資料
軌道週期 P=1.00004回歸年
距離春分點平均離角 ε=280.466457+0.985647358 JD1+0.000304 T2
近地點離角 ω=282.937348+0.00004707624 JD1+0.0004569 T2
軌道偏心率 E=0.01670862-0.00004204 T
軌道半徑 A=1.00001161 AU
計算結果
近日點平均離角 M=ε-ω
利用級數展開的克卜勒方程式(Kepler’s Equation)求得真實的近日點離角
ν=M+360 E sin(M)/π+900 E2 sin(2M)/4π-180E3sin(M)/ 4π
太陽的黃道經度 λ=ν+ω
月球的軌道資料(以黃道面來定義)
月球的平均經度 L=218.316646+13.17639647564 JD1-0.0014664 T2
月球的平均近日點離角 Mm=L-(83.353243+0.11140352394 JD1-0.0103217 T2)
升交點引數 N=125.044555-0.05295376277 JD1+0.0020756 T2
月面軌道傾角 I=5.15668983
擾動修正項
Ev=1.2739 sin( 2L-2λ-Mm )
Ae=0.1858 sin( M )
A3=0.37 sin( M )
修正月球的平均近日點離角 Mm’=Mm+Ev-Ae-A3
Ec=6.2886 sin( Mm’ )
A4=0.214 sin( 2Mm’ )
修正月球的平均經度 L’=L+Ev+Ec-Ae+A4
V=0.6583 sin( 2L’-2λ)
再次修正月球的平均經度 L”=L’+V
修正升交點引數 N’=N-0.16 sin( M )
計算月球的黃道經度與緯度
sin(θ)=sin( L”-N’ ) cos( I )
cos(θ)=cos( L”-N’ )
判斷θ的象限後,求得θ。
月球的黃道經度 λm=θ+N’
月球的黃道緯度 βm=sin-1[ sin( L”-N’ ) sin( I ) ]
若需要月球的赤道經度與緯度,可參考座標系統的變換部分。將黃道座標轉成赤道座標。或者更進一步轉成地平方為角。
範例
2000年9月1日 AM10:30 月球的黃道經緯度 、赤道經緯度 與地平方為角
查得當年力學時與平均太陽時的差值 ΔT=64秒
ET=UT+64秒
計算ET儒略日得到 JD=2451788.60492
JD1=243.60492
儒略世紀 T=0.00667
太陽軌道資料
ε=520.492123
ω=282.948812
E=0.01671
太陽黃道位置計算結果
M=237.543311
λ=158.8947 β=0
月球的軌道資料(以黃道面來定義)
月球的平均經度 L=188.3759761
月球的平均近日點離角 Mm=77.88239044
升交點引數 N=112.14385644
月面軌道傾角 I=5.15668983
擾動修正項
Ev=-0.41717013
Ae=-0.15695074
A3=-0.31254992
修正月球的平均近日點離角 Mm’=77.93472097
Ec=6.14968536
A4=0.08748689
修正月球的平均經度 L’=194.35292896
V=0.62138281
再次修正月球的平均經度 L”=194.97431177
修正升交點引數 N’=112.27901316
計算月球的黃道經度與緯度
sin(θ)=0.98786949
cos(θ)=0.127146
判斷θ的象限後,求得θ=82.66593614
月球的黃道經度 λm=194.9449493
月球的黃道緯度 βm=5.11472622
經過黃道座標與赤道座標系統後
α=13h 2m56s
δ=-1°10′ 7”
經過地平座標轉換後
A=107°
h=30°
白天也可以看到月球!
若是經過多項的攝動計算後,月球的位置會更精確,它的赤道座標位置:
α=13h 1m24s
δ=-1° 2′ 31”
-
http://home.kimo.com.tw/shpao5824/atmosphere.htm
濛氣差修正
由於大氣會對於觀測的星光產生折射的效應,造成觀測星體的位置偏差。由於各地的氣候條件不一,因此要對大氣折射效應的修正並不容易。目前仰角45度以上,有理論直可以直接修正。45度角以下必須透過長期的實際測量來補償。對於仰角45度角以上的濛氣差修正
大氣折射會影響觀測的仰角 Δh=60”.29 tan(90°-h)-0”.0669 tan3(90°-h)
修正後的地平仰角=修正前的仰角+Δh
但是對於地平線的大氣折射值,我們習慣使用 Δh=34′
-
http://home.kimo.com.tw/shpao5824/sunrise.htm
日出與日沒時間計算
季節、地理位置與均時差是日出與日沒時間的主要變化因素。以台灣為例,春分(約3/21日)與秋分(約9/23日),太陽大概是東方出、西方沒。至於夏至(約6/22日),太陽約於東偏北23度出、西偏北23度沒。而於冬至時(約12/22日),太陽則由東偏南23度出、西偏南23度沒。由我編寫的程式,並建立台灣重要地區的高度與地理資料,繪出日出時間的等位面圖。
3月21日的日出時間的等位面圖:

6月22日的日出時間的等位面圖:

9月23日的日出時間的等位面圖:

12月22日的日出時間的等位面圖:

這裡提供一個簡便的方法來計算日出與日沒時間。為了說明方便,犧牲了計算的精密度。用此方法計算日出與日沒時間,大約會有4分鐘以內的誤差。
步驟一
定義日出時間的時角(Hour Angle)
Z=90° 實際的日出,但天色已微亮
Z=96° 民用的日出,一般為街道熄燈的參考時刻
Z=102° 航海用日出時間
Z=108° 天文用日出沒時間,此時天空全黑
步驟二
修正時角
由於太陽有0.5度的視角,因此它的中心點位於地平下1/4度時即可看到,因此實際日出的時角必須加以修正,Z=90.5°
此外因為大氣折射的影響,在地平線下34’的位置,會讓我們以為它正處於地平線的位置。因此實際日出的時角必須再次加以修正,Z=91.067°
至於其它的選項則不需修正日出時間的時角。
步驟三
觀測當日,太陽中午時刻的赤道經度與緯度 (α,δ) ( 請參考「太陽位置的計算」網頁)
觀測者地理經緯度 (λ,ψ)
觀測當日的均時差 E ( 計算方法可參考「時間」的網頁 )
步驟四
τ=cos-1{ [ cos(Z)-sin(δ) sin(ψ)] / [ cos(ψ) cos(δ)] } /15
日沒時間=12+τ+(Υ-λ)/15-E/60 (小時)
日出時間=日沒時間+24-2τ
說明:Υ-λ之中的Υ是指地方時間的地理經度。例如台灣位於東經121°31’38”,Υ=120°,λ=121°31’38”。
範例
2000年9月1日的實際日出與日沒時間?
步驟一
選擇實際的日出 Z=90°
步驟二
修正時角
由於太陽有0.5度的視角,因此它的中心點位於地平下1/4度時即可看到,因此實際日出的時角必須加以修正,Z=90.5°
此外因為大氣折射的影響,在地平線下34’的位置,會讓我們以為它正處於地平線的位置。因此實際日出的時角必須再次加以修正,Z=91.067°
步驟三
觀測當日,太陽中午時刻的赤道經度與緯度 (10h42m29s,8°10’59”)
觀測者地理經緯度 (121°31’38”,25° 4’40”) ( 以台北為例 )
觀測當日的均時差 E=-0.21分
步驟四
τ=cos-1{ [ cos(91.067°)-sin(8°10’59”) sin(25° 4’40”)] / [ cos(25° 4’40”) cos(8°10’59”)] } /15
τ=6.267 hour
日沒時間=18h10m
日出時間= 5h38m
說明:由於我們計算太陽的出沒時刻是以當日中午的太陽位置為基礎,事實上太陽與均時差值無時無刻不在天球上移動,因此我們可以根據初次計算出來的時間,再次修正太陽的實際位置,然後在依此方法重複計算。約三次的修正後,可以得到不錯的精確度,時間誤差應該在分鐘以內。結果如下:
日沒時間=18h12m41s
日出時間= 5h34m42s
-
http://home.kimo.com.tw/shpao5824/contant.htm
天文計算使用的常數
資料來源為天文館出版的天文年鑑
2000年分點常用的星表,使用前需要瞬時分點座標轉換 (參考進動與章動的說明)
?定義常數
光速(c)
299792.458 Km/Sec
高斯重力常數(k)
0.01720209895?導出常數
天文單位(AU)
149597870 Km
秒差距(pc)
3.085678×1013 Km光年(ly)
9.46053×1012 Km
黃經一般歲差(J2000.0,一儒略世紀)5029″.0966
太陽平均赤道地平視差
8″.794148萬有引力常數(G)
6.672×10-11 m3/Kg/S2
章動常數(J2000.0)
9″.2025日心重力常數
1.32712438×1020 m3/S2
黃道傾角(J2000.0)
23°26′ 21″.448地心重力常數
3.986005×1014 m3/S2
光行差常數(J2000.0)
20″.49552太陽年
365.2421903 日
近點年
365.259636 日恆星年
365.256363 日
食 年
346.620070 日?2001.5 年的數值
黃經(一般歲差)
50″.2913
黃道回轉軸的黃經
黃經 174°53′.41赤經(一般歲差)
46″.1248
黃道面回轉速度
0″.4700赤緯(一般歲差)
20″.0430
平均黃道傾角
23°26’20”.746?銀河系
銀河中心(J2000.0)
赤經 17h45.6m
有效直徑
圓盤部份 100,000光年赤緯 -28°56′
銀暈部份 150,000光年銀河北極(J2000.0)
赤經 12h51.4m
厚度
核 心 部 15,000光年赤緯 +27°08′
太陽近旁 5,000光年對赤道昇交點(J2000.0)
銀經 32°56′
總質量
2×1011 太陽質量赤經 18h51.4m
物質密度(太陽近旁)
1.0×10-23 g/cm3對赤道傾角(J2000.0)
62°52′
奧爾特(Oort)常數
A = +15 Km/S?Kpc回轉速度(太陽近旁)
220 Km/SecB = -10 Km/S?Kpc
?太陽
赤道半徑
696,000 Km
色指數(B-V)
+0.65平均視半徑
959″.64
光譜型式
G2 Ⅴ質量
1.9892×1030 Kg
有效溫度
5780°K平均密度
1.41 g/cm3
表面重力
274 m/S2脫離速度
618 Km/Sec.
太陽常數
1.96 卡/cm2?min自轉週期
對恆星 25.38 日
總輻射量
3.83×1026 J/Sec對地球 27.28 日
標準太陽運動(J2000.0)北極方向(J2000.0)
赤經 19h03m
太陽向點
赤經 18h05m赤緯 63°58′
赤緯 +29°實視星等
-26.74 等
速度
19 Km/Sec實視絕對星等
+4.83 等
太陽位置(距銀河中心)
30,000光年?地球
赤道半徑
6378.140 Km
平均太陽日
1.00273791 平均恆星日極半徑
6356.755 Km
24h 03m 56.5554s 平均恆星時扁率
0.00335281
平均恆星日
0.99726957 平均太陽日形狀力學係數
0.0010826323h 56m 04.0990s 平均太陽時
質量比(太陽/地球)
332964.0
自轉週期
23h 56m 04.0990s 平均太陽時質量
5.9742×1024 Kg
自轉速度(赤道表面)
465.1 m/Sec平均密度
5.515 g/cm3
自轉角速度
7.2921151×10-5 Rad/Sec反射能
0.367
平均運動
0.985609°/天?月球
半徑
1738 Km
軌道長半徑
384440 Km平均視半徑
932″.59
軌道離心率
0.0549005質量比(月球/地球)
0.01230002
軌道傾角(對黃道)
5°08′ 47″質量
7.3483×1022 Kg
軌道傾角(對赤道)
1°32′ 33″反射能
0.12
平均赤道地平視差
57′ 02″.6朔望月
29.530589 日
中心差(一近點月)
6°17′ 19″.6恆星月
27.321622 日
出差(31.812天)
1°16′ 26″.5交點月
27.212221 日
二均差(0.5朔望月)
39′ 29″.9分點月
27.321582 日
年差(一近點年)
11′ 06″.4近點月
27.554550 日
月角差(一朔望月)
2′ 05″.2沙羅週期
6585.781 日
近點順行週期
8.8472 年章(19年7潤)
6939.602 日
交點逆行週期
18.6126 年希臘字母
幾次找了辭典查希臘字母的正確用法,卻是難以尋獲.
Alpha
Α
α\r
阿 爾 法
Nu
Ν
ν
妮 宇Beta
Β
β
貝 塔
Xi
Ξ
ξ
克 希Gamma
Γ
γ
伽 瑪
Omicron
Ο
ο
奧米克倫Delta
Δ
δ
代 爾 塔
Pi
Π
π
拍Epsilon
Ε
ε
依布希倫
Rho
Ρ
ρ
羅 宇Zeta
Ζ
ζ
捷 塔
Sigma
Σ
σ
希 克 瑪Eta
Η
η
葉 塔
Tau
Τ
τ
托 宇Theta
Θ
θ
矽 塔
Upsilon
Υ
υ
宇布希倫Iota
Ι
ι
艾 奧 塔
Phi
Φ
φ
伏 伊Kappa
Κ
κ
柯 巴
Chi
Χ
χ
基 伊Lambda
Λ
λ
拉 姆 達
Psi
Ψ
ψ
布 希Mu
Μ
μ
迷 宇
Omega
Ω
ω
亞 美 加 -
樓主的內容應該是轉引自一位台灣朋友的blog,我亦曾經研究過公式
在計算太陽及月亮位置是沒有問題,但計算行星位置就出現重大誤差在計算行星位置時,blog主用木星為例子
計算出的數字:
e=0.0485
m=63.88之後要計算l,公式是:l=m+360.e.sin(m)/pi+900.e^2.sin(2m)/4pi
我照計一次,但不能得出blog主的答案,l=83.3565我想知道是什麼地方出錯,希望有人解答
Log in to reply.